Finding The Next Perfect Square.

I felt like solving this particular kata in python for some reason.

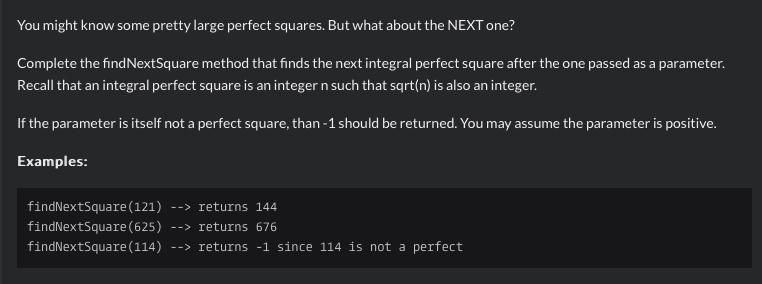
Problem Statement: Essentially, you’ve to find the next integral perfect square after the supplied integral square. If the parameter supplied is not a perfect square, then -1 should be returned.

Sounds simple, and can be solved in many different ways, as pointed out here. But less than about 2-3 solutions are elegant, and precise. Maybe at a later date, I would compare the speed of some of these solutions, when pitted against each other.

Test Cases & Kata.

Python Kata: Finding The Next Perfect Square, Given A Previous One.

View Kata & Test Cases

Here’s How I Solved It, In Python

from math import sqrt
def find_next_square(sq):
    # Return the next square if sq is a square, -1 otherwise
    return  (sqrt(sq)+1)*(sqrt(sq)+1) if ((sqrt(sq)+1)*(sqrt(sq)+1)).is_integer() else -1

The Most Precise, And Elegant Solution

This one’s by lechevalier:

find_next_square=lambda n:-(n**.5%1>0)or(n**.5+1)**2

Here’s another one by AndrewOsentoski:

from math import sqrt
def find_next_square(sq)
	return (sqrt(sq)+)**2 if sqrt(sq)%1 == 0 else -1

On Solving On My First Kata

This problem was my first ever kata. I totally understand now, the reason behind solving a kata. It helps you discover more of/about constructs available in a language, while forcing you to think outside the box. It also helps you compare your code with others, and see what others are doing, and applying as logic to solve a problem.

I do not think that solving katas are harmful; not at all, at this this stage. In fact, I think that I am learning so much, much more about the language, logic, and implementation while solving these. For now, my opinion is leaning towards the for-side of things with respect to code katas. But, this is only the first one solve, and I’ve only just begun. I am still keeping my mind open to whatever I get out of this experiment.

Solve This Kata